
Session 7. Electric currents and magnetic fields
Subjects in any discipline are often compartmentalized and this was so in the study of electricity and magnetism. A magnet has an invisible force field around it which can be visualised with iron filings or small compass needles. Equally an electrically charged object creates a field and this can be displayed with small seeds (I have used dried hay seeds) in castor oil. Various electrode configurations can be studied and it is always seen that the field lines are at right angles to any conducting surface. For many decades the two subjects were kept appart althought it was appreciated that there were many similarities between electric and magnetic fields. However, Newton had energised science and many experiments were being carried out in many parts of the world so breaking down these barriers. For instance, Hans Christian Oersted (1777-1851), a Danish scientist, noticed that a compass needle was deflected when placed near a wire carrying an electric current and hence a linkage occured between electricity and magnetism. This was an exciting time for Physics and one may wish to read the Google book "Electricity and Magnetism - a historical pespective, by Brian Scott Baingrie or a more recent account from https://uwaterloo.ca/phys13news/sites .
Three features about electrical currents and magnetism can be hightlighted : (a) a wire carrying a current produceds a magnetic field, (b) if the current carrying wire is placed in a magnetic field then a force will be exerted on the wire, (c) if the wire (no current) is moved in a magnetic field then a voltage will be developed in the wire. A very good website to explore is that produced at the University of Colorado http://phet.colorado.edu . This site covers many simulations in science and the ones concerning electromagnetism are very informative.
(a) Magnetic fields from currents in wires
In 1820 Oersted discovered the link between currents and magnetic fields. This is illustrated below for a single wire

A compass needle of iron filings demonstrated that a magnetic field was present and the direction of the field is determined by the RIGHT HAND GRIP rule : if the thumb defines the current direction then the fingers lie along the magnetic loops.

Many other wire arrangements can be studied and these are well documented in the literature
(b) Force on a current carrying conductor placed in a magnetic field
Section I is for cases with permanent magnets The a current carrying coductor will experience a force when the conductor is placed in a magnetic field.

The force is given by a simple formula Force = B. i. L where B is the magnetic flux in Tesla, i is the current (A) and L is the length (m) of the conductor . The direction of the force in Newtons is given by Fleming's Left Hand Rule.
An experiment to verify this formula is very simple to set up - a magnet, a coil of wire (150 turns, enamelled copper, diam 1mm) through which a current is passed and a balance for weighing the coil:

And the reading of mass versus current are presented graphically below:

Only approximate calculations, using Force = B.i.L , may be carried out as the profile of the magnetic field within the magnet is not will known. From the graph, a mass increase of 65gm is recorded for a current of 4 A. Assuming g = 10 m/s2 then the magnetic force is 0.65N. With an average value of B as 0.035 T and an approximate value of L as 3 cm (x 150 for the turns) we calculate 0.63 N for the right hand side of the equation. It is only fortuitous that good agreement is obtained since the upper part of the coil will give a repulsive force in the stray magnetic field. The graph shows that there is a linear relationship between current and force as expected.
The great advance that came from this equation was that instruments could be made that allowed currents and voltages to be measured. The diagram of such a moving coil meter is given below

The spring produces a restraining torque proportional to the angular deflection of the pointer.
The current, however, produces a deflecting torque (green vectors) proportional to current since B and L are constant. Thus current is measured by the deflection of the pointer. This type of meter has been used for many years until the arrival of the digital world in the last few decades.
Section II is for cases where the magnetic field is generated by currents in wires. In the second Figure sheet of the session we noted that the currents in a solenoid produced a magnetic field pattern that was very similar to that of a bar magnetand therefore one may anticipate that forces will occur between current carrying conductors.
Two current carrying parallel wires is the arrangment that is usually presented in textbooks as, from this, the ampere can be defined:
The ampere is that steady current which, when it is flowing in each of two infinitely long, straight, parallel conductors with a separation of 1 metre causes each conductor to exert a force of 2x10-7 N on each metre of the other.
The calculation is given below

Figure Sheet


When the two wires are in the form of circular loops the same approach is taken the find the force of interaction. Current elements are chosen from each loop as indicated in the diagram
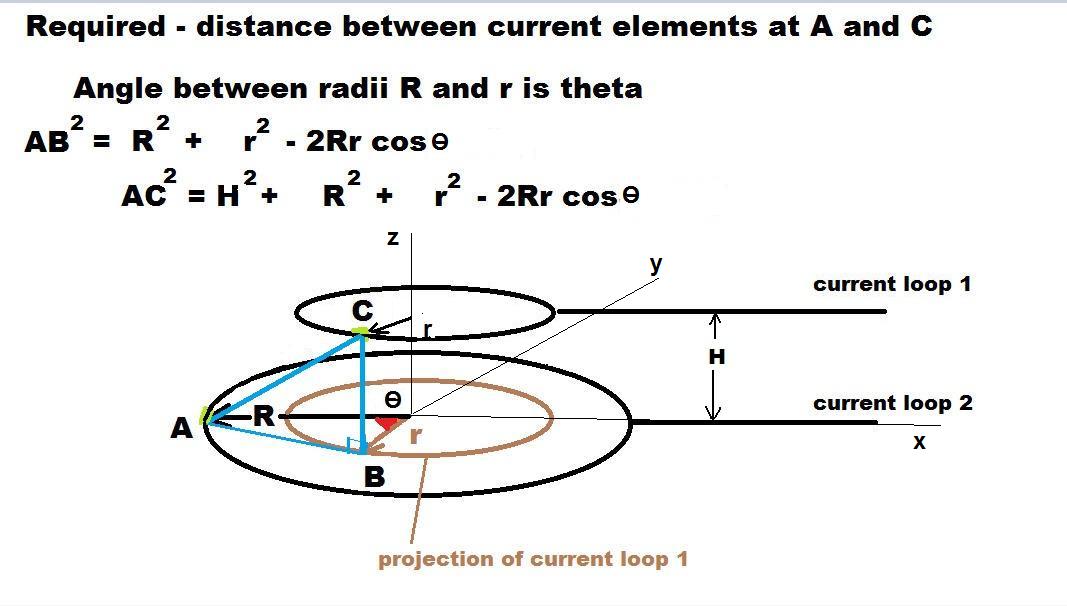
The analysis is discussed by Braneshi et al in their paper "Evaluation of the axial force between two coaxial coils" and the following equation comes from their publication

Unfortunately, the solution of this equation is complex and relies on elliptic integrals. However many texts give approximate expressions and these can be used to estimate the forces between coils.
(c) Voltage generation from wire loops in a magnetic field
The experiments of Oersted and others had showed that "electricity can produce magnetism" but the inverse effect "magnetism to electricity" had to wait over TEN years before it was discovered. This could have resulted from feelings that steady currents and voltages were anticipated and we now know that electromagnetic INDUCTION requires a changing magnetic flux. History usually credits Faraday (1791-1876) with the discovery of electromagnetic induction despite the fact that Henry (1797-1878) had made the same discovery a year before. However, a paper presented by Faraday on 24th Nov 1831 to the Royal Society is generally taken as the date of discovery.
Faraday stated that
The magnitude of the induced emf (electromotive force) in a circuit is directly proportional to the rate of change of magnetic flux linkage. The direction of the emf is given by Fleming's RIGHT HAND RULE as the following diagram shows

If the Colorado site is opened http://phet.colorado.edu then Faraday's Electromagnetic Lab may be selected from the Physics section. One is invited to "Play with simulations" then download and open .

After a short loading time there is a full screen presentation with five options "Bar Magnet", "Pick-up coil", "Electomagnet", "Transformer" and "Generator". The "Generator" depicts a water-powered unit where the bulb is illuminated periodically as the magnet is rotated.

The "Transformer" shows that no emf is generated until the primary is changed to an alternating source ( slide voltage button back and forth) .
Have fun .... and a special thanks to Phet for making the simulations available.
Induction effects are described in two recent articles :
The shaking torch , Physics Education 2010, Vol 45(5) p578, An inductive probe for measuring the Earth's magnetic field, Physics Education 2014, Vol 49(5) p 489.
A bike generator is demonstrated with a very simple arrangment of permanent magnets and coils - Luke, my grandson, is providing the motive power.

The coils were each 180 turns of enamelled copper wire and connected in series (wire diamameter 1 mm)

A working model is shown in the video clip.
The inter-twining of electricity and magnetism has resulted in a general title being used to embrace both topics , namely, "electromagnetism" . This is the third element of classical physics (together with mechanics and thermodynamics) that propelled the scientific world into the ninetheeth century. Many more exciting areas of physics were yet to unfold as the Quantum World became a reality.
We can conclude this session with words attributed to Michael Faraday;
" the beauty of electricity and magnetism .... is not that they are hidden or mysterious....but that they both obey physical laws"