
Session 2 Motion, little g and big G , and things MECHANICAL & Rockets
Motion
Motion is everywhere; it is so obvious that we don't even bother to think about it. However, in Physics we need to quantifiy ( say it in numbers) all our observations so we will think about motion. For starters lets consider a short car journey

We assume that the road is level and straight and we start with a velocity of zero . We then accelerate to a speed of 13 m/s ( or ms-1) in 40 seconds. Using the formula v = u + at we can see that our acceleration is 0.325 metres per sec per sec:. This formula follows from the definition of acceleration and is referred to as the First equation of motion. In terms of notation we could write a as m/s/s but this may be confusing so we note that acceleration a has units ms-2. For the next 80 seconds there is constant velocity but then we have traffic lights on RED and have to stop. Using the First Equation of motion again we see that a is now -1.3 ms-2. A negative value simply means that we a slowing down. We wait at the lights for 40 seconds then accelerate to a higher speed of 16 m/s and then slow down to complete our journey in 300 seconds.
(A, 0 ; B. 40; C, 120; D. 130; E, 170; F, 205; G, 260; H. 300 are the respective times for the journey)
From the area under the graph we can see how far we have travelled. B-C , D - E, and F-G are regions of constant speed so the distance travelled is just the area of a rectangle ==== B - C gives 1040 m ; D - E gives zero ; F - G gives 880 m. For the other region we use the area of a triangle formula ... 1/2 base x height ... A- B gives 260; C - D gives 65; E - F gives 280 ; G -H gives 320 . So the total distance travelled is 2845 m.
We could look again at the initial part of our journey A to B. In general terms the base of our triangle is t and the height is v. But we know that v = at as the initial velocity is zero. Thus, we now have a general equation for the area of the triangle s = 0.5at2 . It is relatively simple to show that if an initial velocity u had been present then the full distance equation would have been s = ut + 0.5at2 . This is known as the Second Equation of motion. Usually, there is a Third equation written down but this only needs to be derived from the other two by a little algebra
We square both sides of the first equation .... v2 = u2 +2atu + a2t2 ... then v2 - u2 = 2a(ut + 0.5at2 ) = 2as
Summary
Equations of motion
(1) v = u +at
(2) s = ut + 0.5at2
(3) v2 = u2 + 2as
Now, Sir Issac Newton (1642-1727) put motion onto an even firmer footing by announcing his Laws of motion:
1 Every body continues in its state of rest or uniform motion in a straight line unless acted on by a force
2 The rate of change of momentum is equal to the applied force
3 Action and reaction are equal and opposite
Now MOMENTUM is just mass x velocity and so the second law reduces to F = ma if m does not change with time. From the third law we find that, for any interaction ( a collision, say), we have : - MOMENTUM BEFORE (collision) EQUALS MOMENTUM AFTER (collision).
The acceleration due to gravity is so special to people living on this planet as it is responsible for the force pulling each one of us down to earth. It is therefore given a special symbol "g " and has a values close to 9.81 ms-2 .
Now that we have introduced FORCE ( measured in NEWTONS) it is time to introduce ENERGY. After all, in our car journey, we know that the car burns fuel and that chemical energy in the fuel has made the car move.... it has been changed to heat energy in the cylinders and then to mechanical energy by the pistons in the car being forced up and down.
However, we can think about a much simpler example to illustrate energy at this stage by supposing we carry a rock up a cliff as shown

The work done is just APPLIED FORCE x DISTANCEover which force is applied
So in our problem of lifting a rock up a cliff the force is just that which balances gravity mg and the distance is h giving mgh as the work done. We now say that the rock has potential energy and the term "potential" expresses an ability of this energy to be released at a later time. (In everyday life we use this term -- if I said to someone "you have the potential to be a good runner" then I wouln't expect that person to show me their running skills immediately but, at some time later, when they were running I would expect them to run quickly.) Now we see what happens when the rock is released ---- we have our Third equation of motion v2 = u2 + 2as We can simplify this as u is zero and a is now called g and s is written as h so giving v2 = 2gh
If we now multiply both sides by m and divide by 2 we see that 1/2 mv2 = mgh . Well, the right hand side of the equation is just potential energy and the rock has this at the top of the cliff. By falling to the beach the rock has acquired a different form of energy, kinetic energy (energy of motion) and we know full well that the rock will bury itself in the sand. By doing this all the kinetic energy will be converted to heat and and the thud we hear is sound energy.
As a summary Potential energy P.E. = mgh
Kinetic energy K.E. = 1/2 mv2
Energies are measured in Joules - a name chosen to honour James Prescott Joule (1818-89) an engineer/scientist who lived in the Manchester region, UK.
(note Please do not conduct a real experiments like this as there may be someone on the beach below !!!!!!!)
Another important feature of carrying the rock up the cliff is how fast we do it - if we run up with our rock then we will be out of "puff" when we get to the top. The quantity that tells us how fast we are working is POWER or Joules per second - or Watts , ( in honour of the Scottish inventor, James Watt 1736-1819)
( Maybe we can remember the term power by thinking about "how much puff are we using" !!!!!
Most problems in MECHANICS can be tacked with the equations given above so you are now able to understand how motion works.
Ann-Marie has prepared lots of examples ::: Trampoline Trampoline.pdf and Children's play area Ann-Marie_Pendrill_2005_Phys._Educ._40_527.pdf
A little practical work will now be attempted
After reading session1 you can appreciate how important it is to do experiments in Physics; experiments have to be done before theories can be formulated - so let's start.
Big G, the gravitational constant that Newton introduced, is a fundemental constant of the universe but little g is closer to home; it is the acceleration that any object will have if it is dropped off , say, a cliff. We all know that Newton's second law of motion tells us that -- Force = mass * acceleration. So any object has a force pulling it to earth with magnitude m*g .
It doesn't take much mathematics to see that Newton's gravitational law, F = G (Msun mplanet) / d2 , gives a direct link to little g since the same formula can be brought down to earth. In place of the mass of the sun we put the mass of the earth and in place of the mass of the planet we put the mass of any object situated on the earth's surface -- then we have :-
g = G* mass of earth/(radius of earth)2 since the earth's attractive force comes from it's centre.
using values G = 6.67*10-11 Nm2kg-2, mass of earth = 5.98*1024 kg and radius of earth is 6.37*106 m we get g = 9.83 ms-2 . This value is a little different from that quoted earlier as the earth is not a perfect sphere and g = 9.81ms-2 is a measured value.
The experiment to measure g is simple -- an object (tin of beans if you like), a piece of string and a mobile phone which has a stopwatch as one of the applications ("apps") .
Secure the object at one end of the string and fix the other end to a support that will take the weight of the object ( say the edge of a work surface in the kitchen). On moving the object from it's rest position one can observe an oscillating motion ie we have made a pendulum, and the oscillations will last for a few minutes. Now all we have to do is find the time of one oscillation T, and measure the length of the string from the centre of the object to the support. An equation which is given in all Physics textbooks reads as follows --- ------ T2 = 4* ( pi )2*L/g ---- so by knowing L and T the value of g is determined.
**********************************************************************************************************************
My experiment gave the following results Time of ten oscillations was 18.3 sec (remember !!!!start counting from zero) giving T = 1.83 sec and the length of the string was 0.80 m. A calculated value of g is 9.42 ms-2 .
A serious physicist will now ask "how reliable is the measured result?" The timing of a single oscillation would be difficult to measure so the strategy of timing 10 oscillations has given an improved accuracy. But one will see that this time can have a value anywhere between 18.1 secs to 18.5secs so there is almost a 2% inaccuracy with regard to timing. The measurement of length is even more problematic as the one has to measure the distance between the support and the centre of gravity of the object . The inaccuracy here will be more like 3% so that a total accuracy of no better the 5% is expected. Thus, the best we can claim is that g has a value between 9.0 ms-2 and 9.9 ms-2.
**********************************************************************************************************************
If you have chosen to complete the experiment then you have joined the company of illustrious scientists such as Galileo. You have also confirmed the notion that all bodies are acted on by the gravitational force. Aristotle had given the false hypothesis that matter on earth is made up of four elements - "earth", "air", "fire" and "water "- and this affected the manner in which they fell to earth. Stones would fall quickly as they had a lot of "earth" in them whereas a feather would fall slowly as it had "air" in it. The lunar Appollo crew made a convincing experiment on the moon in which a hammer and a feather were dropped from a height of about 1 m. As expected, both arrived at the surface of the moon at the same time and the only reason why the hammer and feather experiment cannot be repeated on earth is that air friction retards the motion of the feather so that a hammer/stone will always arrives at the earth's surface before the feather. (The lunar experiment can be followed on Utube)
In January of this year (2014) an interesting article was published in the Physics Education journal describing an inductive gravimeter (page 41, volume 49). By using electronic timing the free fall of an object could be investigated. Full details are given in the article but the essence of the method is that the object is a magnet and, as it falls through a series of coils wound on a tube, an induced voltage is recorded on an oscilloscope . The advantage of this experiment ( as opposed to the pedulum experiment above ) is that it clearly shows that the object is accelerating and therefore g becomes very much part of the equations of motion.
A metre long cardboard tube was used, 45 mm OD and 40 mm ID. Fifteen coils, 10 turns each, were wound on the outside and were all connected in series; the spacing was 5 cm between the centre line of the coils and an illustration of two of the coils is given.
The illustration shows that the coils are series connected with the left hand wire continuing from coil to coil. The return wire on the right hand side comes from the fifteenth coil at the lower end of the tube (note the wire is insulated copper and has a diameter of 0.052 mm).

A Picoscope ADC100 is used to record the induced voltage and a "single shot" mode is used. Results are presented below and it is clear that these times could never be made with a stop watch.

The trace clearly shows that the magnet is moving faster and faster as it is acted on by the gravitational force.

The magnet N_S poles give rise to positive and negative swings in the induced voltage and, from an EXCEL trace the times of the middle point can be determined. We know that these cossings will occur just when the magnet passes the coil so a time versus "fallen distance" of 0.05 m, 0.10 m, 0.15 m ....... can be plotted. From the laws of motion we have s = 0.5*g*t2 + u*t so the data can be fitted to a polynomial of second order.
We therefore find that the falling object method gives g = 8.4 ms-2 . One can only state that no allowance has been made for air resistance in our theoretical framework and, as we see with the feather, this can be considerable. Thus a value of g = 8.4 ms-2 is an acceptable result.
Little g is the topic of a recent review article by James E Faller at the National Institute of Standards and Technology (NIST) which covers the subject in greater detail.

The measurement of Big G is sometimes neglected in student's Physics courses as this experiment requires quite a lot of patience and care. There was a flurry of excitment in the scientific community several years ago when it was rumoured that the gravitational force might not be exactly inversly related to the mass separation squared. Several elegant measurements were carried out in many Laboratories but all failed to show any discrepancy with Newton's formulation.

Leybold didactic have always provided apparatus of outstanding quality and their apparatus is usually used to measure G. Comprehensive leaflets are provided as illustrated:-

Newton's pronouncement in Principia of his gravitational theory was the staring point of science and we shall see that theory and experiment go hand in hand through the scientific story. With the discovery, recently, of the Higgs boson we have to realise that sometimes the experiments will get very complex and theory has to wait some years for verification. We all know that Newton didn't have the last word on gravity and that Einstein developed the General Relativity Theory which is currently accepted as a more complete theory for gravity. At a summer school in 2007 Martin Hendry presented a paper "An Introduction to General Relativity, Gravitational Waves and Detection Principles" which is a good 96 page read???? On page 88/ 89 he shows how the precession of planetary orbits follows naturally from Einstein's theory but was impossible to predict from Newton's Gravitational Theory.
Mechanics
Once the idea of forces and gravity was understood the wonderful subject of Mechanics could begin. A very helpful text book is "Mechanics" by R C Smith and P Smith Wiley 1973. Just two examples will be given here --- water power by an Archimedes Screw and Rocket propulsion.
Water power.
Now this wonderful thing called Gravity can do work for us .....
If you carry sacks of grain up a ladder into the granary then you will soon get puffed out so it is obvious that you are doing work. But if you let the sacks fall down the ladder then anyone at the bottom will be severely squashed showing that the sacks have gained quite a lot of energy by falling...gravity has pulled the sacks down and given them energy.
With water power the early water wheels were essentially buckets fitted to the rim of a wheel and water was poured in at the top and emptied at the bottom and each falling bucket full of water gave us energy (and Style Mill, Manchester, is an example of this).
The Archimedes screw was invented thousands of years ago and used for just the opposite process of lifting water UPWARDS into irrigation channels. Only in the last ten or so years has it been used for generating power - each little segment is just like a bucket and this moves from a high level to a lower level and so produces power in the form of rotation. We need a Gear Box and a Generator and then we feed the power into the mains.
In some cases you could used the energy on site (grinding corn for instance or running a refrigeration plant, say ) but, more often than not, the "mains" act as a battery .....
BUT we have to get our frequencies to match- this is done with a variable speed drive so that - whether the screw is turning quickly or slowly the output is always 50 Hz.
The water wheel is only of historic interest now and other devices for abstracting water energy are illustrated below:-

As one can see the Archimedes screw is the preferred turbine for low flows and low heads of water. Thus, all the sites in the UK where water wheels previously existed, during the industrial era of the seventeenth and eighteenth century are ideal sites for an Archimedean screw to be installed and hopefully work will continue apace to give Hydro-power a larger share of the renewable energy program.
And now we can do a little maths
Energy and Work amount to the same thing and we all know the work comes from moving a force over a distance. Energy from water is therefore generated by a mass of water, m, falling through a height h. As above, we wrote -- force = mass * acceleration --so the potential energy is given by m * g * h . Power is simply the energy generated per second as the following diagram shows:-
In one second the front end of the cube of water covers a distance 1m downstream from the weir and the trailing end just manages to fall over the weir. So, all the volume of water (inside the cube) falls 1 m and the mass can be calculated knowing that the density of water is 1000 kg m-3 . Also knowing that little g is about 10 we can see that the energy generated in 1 sec is 10,000 Joules which, of course, is 10 kW. In each particular installation of an Archimedes Screw the volume of water will be different -- so we can write a general equation speed (m/s)* fall (m)* width of channel (m) and then this volume is multiplied by the density (=1000 kg/cubic meter) and little g (=10). The purpose of the screw is to let the water fall in an orderly manner and convert the potential energy into kinetic energy of rotation and so "power" an electrical generator. The conversion is moderately good at 20 % to 30 %.
A 40 kW installation is pictured below:

Stockport Hydro is a community project that has been generating power since Oct .2012. In a good week the output will be close to 7 MWh -- ie-- 1 MWh per day. Now, suppose at home we left a lamp with a 100 W bulb switched on for the whole day then we would consume about two and a half kilowatt hours so our Archimedes screw could keep 400 such homes supplied with electricity. Generally, our consumption will be higher and so more like 100 homes would be supplied.
But like any of the renewables a power input from the screw does help to save burning valuable hydrocarbons and so reduces carbon emissions.
Remote control is a very helpful feature of the installation:

Together with numerical data most of the sensors also give a graphical display so that trends over the day can be recorded

The wonders of water power are best illustrated at Cragside, Northumberland. The property is now in the hands of the National Trust (www.nationaltrust.org.uk) and they are continuing Lord Armstrong's love of water power with exhibitions and working models. A water wheel and a small Archimedes screw are shown below:
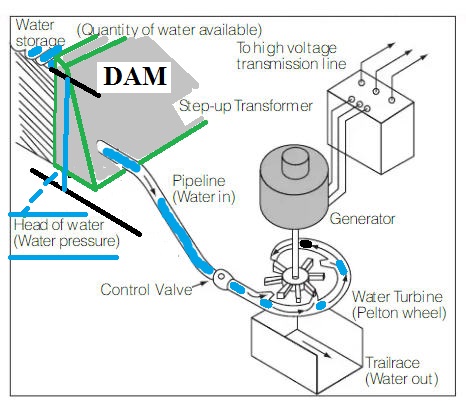
An illustration of a Pelton Wheel is given below as this mechanism is so useful if a large head of water is envisaged. Provided that the water pipe can withstand high pressures the head of water can be at least 100 m above the water outlet so generating a large power.
Rocket propulsion
Do you have to be a rocket scientist to understand rockets? Possibly not, although I can well remember that most of our class found it difficult at school. Our main dilema was that we felt " there was nothing to pull /push against in space" . For instance, someone in a swimming pool has the water to pull against to move forward and aeroplanes are pulling against the air even though this is not a very dense material. In space, however, there is nothing to pull against!!!!! Some long time after this school experience I watched the Open University videos when they were at an ice rink to demonstrate the law of conservation of momentum. It was then obvious that one "pulls/ pushes against the matter that is ejected". If there are a couple of people stationary on the ice and either person pushes the other person away then their video clearly shows that one person moves forward and the other moves backwards; momentum is conserved : it was zero before the push and zero after and that is how momentum has to be in space. The diagram below shows how 9 'bits of rocket fuel" are pushed away to give the green "capsule" plus astronaut a forward motion.

Ignited fuel will always leave the rocket with the same speed, v, with respect to the rocket. So we see that with the first blast of fuel the rocket has a speed of v/9 . Our coordinate system on board the rocket has been the same as that for any person watching from the launch pad; both would observe a "before" speed of zero. But very soon we appreciate that the launch pad is out of view and we would then be attuned to the capsule/ rocket coordinates.
The Physics of this first burst of fuel dictates that conservation of momentum holds - "momentum before "= "momentum after", so we have 0 = mv + 9*m * Vrocket . (Just like the situation at the ice rink, the rocket moves with v/9 in the opposite direction to the fuel.)
Note -- Changing coordinate systems is not something too strange -- as a regular commuter into Manchester, I do it every day though I don't usually think about it . I get on a train and, after pulling out of the station (and feeling an initial force), I hardly know that I am moving . Indeed, if an "up" train and a "down" train stop in a station it is quite difficult to known which train moves off first if one is looking at the adjacent train.
In just the same way an astronaut will link his/her coordinate system to the capsule. He/ she will appreciate that an impulse to a new speed of v/9 has occured (and things may rattle a little on board the craft) but the speed is zero within the spacecraft and for all the remaining 8 portions of fuel still present in the rocket. Of course, using this new frame of reference we will know that the person on the launch pad is moving away with a velocity of - v/9.
So, we can start with our new coordinates tied to the rocket/spacecraft and it is obvious that our our first diagram can be repeated and a momentum equation is again written down. As before, we draw a "before" and "after" diagram but now with a new initial mass (astronaut plus fuel is now 9*m). ----- so---- 0 = mv + 8* m*Vrocket and the rocket will move with v/8 in the opposite direction to the fuel. Now someone watching from the launch pad will see the rocket going faster as it already had a speed of v/9 so now it will have a speed of v/9 + v/8 . If this procedure is repeated, ie updating our cordinates to be with the astonaut after each impulse then all NINE fuel ejections can be covered and we find that the final rocket speed is a summation: v/9+v/8+v/7+v/6+v/5+v/4+v/3+v/2 +1*v (=2.826 * v ) as viewed from the launch pad , The correct theory gives a formula (page 166 Smith and Smith ) Vrocket = v * Natural Log ( 1 - 9/10) == 2.3026*v .
Note, if the fuel had been ejected all at once the rocket speed would have immediately jumped to 9*v but neither rocket nor astonaut would have survived. If two fuel burns had been employed we would need to parcel up the fuel differently 4.5*m and another 4.5*m with m remaining as the capsule.So 4.5*m ejection at first with 5.5 mass to be moved forward: 0 = 4.5 *m*v + 5.5 *m*V -- so V for the rocket would be 0.818*v . Then the next 4.5*m would be burnt off and this would give 4.5*v in rocket coordinates. ( this last burn would again kill our brave astronauts and all the instruments !! ). So we see that the final rocket speed as viewed from the launch pad is about .82*v + 4.5*v , ie Vrocket , would be 5.32*v (this last value is somewhat smaller then the single burn value and so I hope you will agree that it is therefore not unexpected that a continuous burning of fuel will lead to 2.3026*v as given by Smith and Smith. They also provide the full theory of rocket propulsion on pages 166 /169 and show that it is necessary to have a two stage rocket to leave the earth's gravitational field.
Believe it or not the UK were developing rocket technology in the 1950's
Here's the story behind a UK top-secret facility
In the 1950s Britain was still a "great power" with a large empire but the new "superpowers" of USA and USSR were dwarfing the UK as "movers and shakers" of the world. However, the newly developed UK nuclear weapons needed delivery systems. The British government ordered the invention and construction of an inter-continental ballistic missile, code named "Blue Streak". The job fell to the Royal Aircraft Establishment at Farnborough. They began an intense effort to research, develop and deliver the required technology. Their findings identified the engine-makers Armstrong Siddley and the aircraft designers Saunders Roe whose company was situated at Cowes, Isle of White.
The Blue Streak would be preceded by a smaller prototype rocket that used the same complex liquid propellants but employed hardware and techniques that were immediately available. This rocket was Black Knight. In 1955 Saunders Roe of Cowes were commissioned to develop the air-frame and to carry out the assembly and testing of the missile. They were developing a mixed power-plant fighter aircraft, the Sr53. This employed a rocket motor which ran on kerosene and high-test peroxide.
With engine makers Armstrong Siddley, Saunders Roe adapted this motor for space operations and evolved special methods to fabricate the large, lightweight tanks needed to hold the propellant which made up some 90% of the rocket's total mass. Of special concern was the need to maintain cleanliness and chemical purity when dealing with high-test peroxide which reacts rapidly with most substances by violently separating into very high temperature steam and oxygen. The high-test hydrogen peroxide (H3O2) ignited instantly on contact with kerosene into super-heated steam that could propel the missile faster than the speed of sound, but with an almost invisible flame wake.
The role of the Isle of Wight test site
To assemble and test each rocket before shipment to the Australian launch site at Woomera, Saunders Roe required a local test site. The former artillery battery on the Needles Headland offered a secure location with underground accommodation. In 1955 the High Down site was leased from the Ministry of War. Here, from April 1956, the engines were assembled, tethered and fired, with different levels of fuel to measure the thrust, flight control systems and the consumption of the fuel.
The Needles Headland was transformed into something like a James Bond film set. A complex of specialized buildings was constructed over the New Battery, and underground control and instrumentation rooms were converted from the old magazines. There were 2,200 square feet of control rooms and underground stores, 4,260 square feet of laboratories and offices and 3,080 square feet of workshops and smaller machine shops. The dining rooms catered for 80 people at a time. In all there was space enough for the 240 people who worked there at the peak of operations in the early 1960s.
The 60-foot-long rockets were assembled in the workshops. Then they were towed down the newly built road along the cliff top above Scratchells Bay to one of the two 80-foot-high test gantries. These stood at each side of the natural bowl in the cliff formation above Sun Corner. The rockets were erected inside the steel and aluminium towers by men dressed in protective suits with glass fronted helmets, operating one and a half ton mobile hoists.
During an engine firing test all activities followed at a strict time sequence, initially co-ordinated by large clocks placed at all manned positions. At any point the process could be aborted by the press of a button from several monitoring positions. As the black hands ticked towards the red section of the clock face, the clocks bleeped every ten seconds to warn the workers to get underground. There the scientists stared into an array of "huge grey instrument panels, covered with flickering lights, cathode ray tubes and multi-coloured switches and plugs."
In addition to manual observations, an array of cameras, tape recorders and specialized devices automatically logged data from several hundred instrumentation sensors placed within the engine and other rocket systems to assess their performance.
On ignition the four jet rocket motors fired into steel "exhaust buckets," cooled by a torrent of water from a specially built 60,000-gallon reservoir, at a rate of 3,000 gallons per minute. The exhaust emerged at right angles from the cliff as "a fountain of steam" as the late Vera Attewell recalled, seeing it from the sea, but it only sounded "like a wet squib." At this point the only thing stopping the missile flying through the roof of the gantry was a steel golf-ball coupling in the engine structure clamped to the test bed. The local population were warned of the firings and the downs were closed to the public, "as far back as Tennyson's Monument at least once to my knowledge" recalls Derek Mack, who worked on the project throughout.
With the missile successfully tested a team of engineers accompanied it to the top security missile launch-site at Woomera in Australia. In 1958, after just three years' work, they released the first Black Knight into the atmosphere. In all 22 were launched into moonless night skies, up to 500 miles above the Earth, falling back to land 80-100 miles down-range of the launch site.
Despite this success Britain eventually gave up on Blue Streak and acquired Polaris missiles from the USA. Black Knight became a tool for research into the upper atmosphere, flying payloads for government agencies and universities. This work suggested the need for Britain to develop a capacity to launch satellites, which led to the next stage of the space programme.
The Space Satellite Programme
In 1965 the Needles team started work on Black Arrow, an 18 ton, almost 44 foot, three-stage space-rocket designed to put a 300-kilogram satellite into a circular 300-mile orbit. The first two stages were designed to reach the right orbital height; the third blasted the satellite at right angles to the Earth's surface, with sufficient velocity to put it into an orbit of continuous free-fall.
Six Black Arrows were built and four launched into space, the first in 1968. The project culminated in October 1971 with the launch of the first, and only, all-British satellite put into space by a British rocket. The experimental satellite Prospero achieved a near perfect orbit and carried out short term data collection on micro-meteorites and space erosion.
Having achieved its peak, the British space programme suddenly ended in a lack of political will and scientific consensus on how to use the rocket. The Needles rocket site was closed, and the buildings dismantled. In 1979 the Woomera station was demilitarised.
The last Black Arrow now resides at the British Science Museum. Another reminder is Prospero, which still functions when contacted from Earth, and will continue to orbit us for another 220 years.
Almost 50 years on --
(Mr Richard Branson is, no doubt, well versed in rocket science and when the Virgin Galactic space vehicle makes it's maiden flight then it will be the start of an era of "space flights for all" and we will all have to become well versed in rocket (science (see guardian weekend 22-02-2014)....... It is sad to report that a crash took place ( see Guardian 1Nov2014 ) killing co-pilot Michael Alsbury and leaving Pete Siebold injured after parachuting to the ground . Mr Richard Branson was devastated by the accident but insisted that the project must proceed with safety being at the forefront of all future test flights..
It is exciting to report that a succesful launch was carried out on 11 July 2021and that "space" is now open for business Click here .
Perhaps I could end this session with a machine that started off the whole evolution of Industrial Society. For all my school days I was ferried down to Whitby by steam trains and, undoubtedly, Steam Power holds a special place in my heart --- why not click here ?